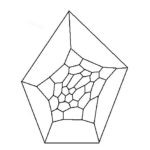
四色問題(四色定理とも言う)という問題があります。
これ、「発展問題」として最適だと思うので、お勧めします。
4色問題とは、「平面上の地図は4色で塗り分けることができる」という問題です。
ド・モルガンという数学者が、1852年に書いた手紙よりこの難問は誕生しました。
以後、120年あまり数学上の未解決の問題として多くの数学者を悩ませました。
結局、1976年コンピュータを駆使することによりやっと解決したのでした。
子供たちに示すのは、この定理を使って色を塗るという課題です。
向山洋一氏が、学習ゲーム的な発展問題として紹介しています。
「「向山型算数」以前の向山の算数」 向山洋一全集24
実際にやってみると、けっこう楽しいです。
これはどこから塗りから始めてもいいので、とりあえず始めます。
次の場所は違う色になります。
その次は、残り2色のうちどちらを選ぶかっていうと、迷うんですね。
でも、接しているところの数を数えることで、色が決まるのです。
というようなことを考えて、けっこう頭を使って楽しいのです。
これ、ざっくり言いますが、3年生以上ぐらいでできると思います。
ぜひ、プリントしておいて、課題がはやく終わった子にやらせてください。
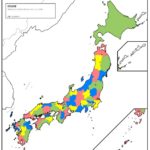
そして、最後は、日本の都道府県を四色で塗らせたいです。