ローカルな話題で申し訳ないのですが、先日、京浜急行線に乗ったら日能研の「シカクいアタマをマルくする」問題が車内に掲載されていました。 「東急だけではなく京浜急行にも載っているのか」と思わず問題をのぞき込んだら、そのまま問題を解くことに夢中になってしまいました。
その問題です。
問題文
何人かで旅行へ行き、写真を3枚撮(と)りました。
1枚目の写真には3人、2枚目の写真には4人、3枚目の写真には6人写っています。
3枚すべてに写っているのは1人、3枚中2枚に写っているのは2人であるとき、旅行へ行ったのは全員で何人でしょうか。
ただし、写真に写っていない人はいないこととします。
2018年 昭和女子大学附属昭和中学校入試問題より
https://www.nichinoken.co.jp/shikakumaru/201808_sa/
これって、どう解いていきましょうか。
私が、まず考えたのは「つるかめ算」のようなやり方です。
「つるかめ算」は、全部がかめだったとして計算します。その上で、最初に示された匹数と比較して、つるの数に変えるのです。
ここでは、重なって写ってる人が一人もいなかったらどうなるのか、をまず考えます。
すると、3+4+6=13ですね。
でも、本当は、3枚に写っている人が1人いて、2枚に写っている人が2人います。
ということは、13人は重複しているので
す。
13-2=11(3枚に写っている人の重複分を減らす)
11-2=9 (2枚に写っている人の重複分を減らす)
すると、9人が答えとわかります。
私がもう一つ考えたのは、「しらみつぶし」に答えを探すということでした。
「しらみつぶし」と言っても、3枚とも写っているのは1通りしかありません。
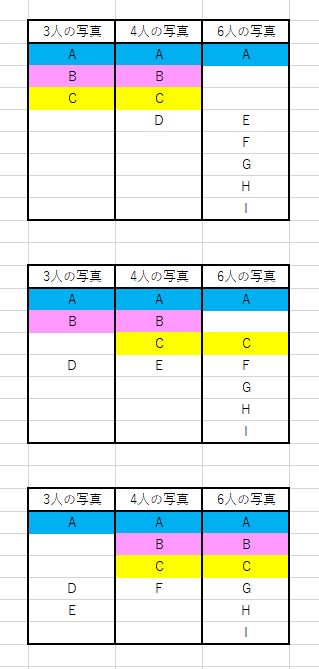
問題なのは2枚に写っている人です。この場合は、3通りあります。
私はこの3通りを、みんな書き出したのです。
画像にして添付したのでご覧ください。
やってみると、やはり9人が答えとわかります。
他の解答方法を日能研が示していますので、それもご覧ください。
この問題は、難問として56年生あたりにやらせたら楽しいと思います。
要領のいいやり方でも、体力派のやり方でも、どちらでも解答できます。